A theory of relativity already governed Newtonian mechanics. It’s impossible according to Galilean relativity, to perform a mechanical experiment that tells one if she is in constant motion or at rest. Galileo’s transformation equations were as follows
A problem became apparent when Maxwell published his equations of electromagnetism. He discovered that the speed of light is constant and propagates through an "aether". Motion through the aether of space is absolute and not relative and thus one could discover using light rays if they were traveling at a constant motion or at rest, violating Galieo’s thesis. The Michelson-Morley experiment was the failure to detect such motion. Something was obviously wrong.
Galileo had not understood the effects of time dilation and length contraction. Today most physicists explain these effects as simply the result of time and spatial coordinates. These are not invariant and change from coordinate system unlike proper coordinates. Lorentz transformations are supposed to rotate these coordinates.
Lorentz, Larmor, FitzGerald and Poincare tried to explain the effects as the result of motion through the electromagnetic field. Since material objects are bound together by electrical forces its natural to consider that they themselves should be affected by motion through space. Our question "can a Lorentz aether theory explain the Michelson-Morley experiment?" is in fact equivalent to "can these effects be explained using the electromagnetic field?" John Bell showed that the answer was in fact yes.
Lets limit ourselves only to a simple example, a hydrogen atom with one electron moving along the z axis. Consider what happens to the orbit of the election. When the atom accelerates in an electric field our motion equation is
Where r is the position of the election in the field. At high velocity the familiar momentum equation is unsatisfactory.
Provided that acceleration is smooth. the nucleus will experience FitzGerald contraction in the direction of motion and the orbit will appear elliptical rather than circular. This orbit will now occur over a period larger than the original, such that it experiences Larmor dilation. The total number of orbits for a time t with velocity V(t) is given by
This suggests that we should describe the variables of the system to incorporate these effects.
The moving orbit described with the primed variables is the same as the stationary orbit. One can extend this description to the field of the uniformly moving charge. During any orbit
One only has to take a suitable origin for z and t in order to derive the standard form of the Lorentz transformation equations.










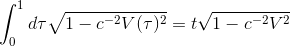
Comments
Post a Comment