John von Neumann's argument for quantum logic was based on the Hilbert space formulation of quantum mechanics. In essence a Hilbert space is the quantum analog of phase space used in classical mechanics. In quantum mechanics the basis of interest are not just classical variables like position and momentum but also include spin and super positions of those variables. If there are N possible states a system can be in, then the Hilbert space of that system is the collection of all possible super positions of those N possible states. Where the sub space of a Hilbert space represent the properties of a given quantum system.
Consider the following 2-Dimensional Hilbert space for particle of half integer spin (all given in units of reduced Planck's constant)
Quantum mechanics uses complex, rather than real Hilbert spaces but this will be sufficient to illustrate von Neumann's argument.
In the Hilbert space the component P is a projection operator and operators orthogonal to each other represent "non community operators" which are incompatible properties of a quantum system.
If P is a projector we can represent its negation as
Now simply, the components P refers to a particle with spin in the z-direction.
What's unusual about the Hilbert space that's not corresponded with the phase space in classical mechanics is that it represents other properties too. For example in the diagram above, Q is the particle's spin component in the x-direction
Every ray in the Hilbert space represents some value of the spin of the particle which leads to an obvious problem for quantum mechanics. To understand this lets relabel the positive spin in the z-direction with the label P and the negative spin in the x-direction, Q. How do we represent the conjunction of P and Q? In propositional logic the answer is
In propositional logic the conjunction of two contradictories is false, the problem in quantum mechanics is that it's not even false. The statement is undefined because it cannot be represented on a Hilbert space. Von Neumann and Birkhoff began applying different rules to quantum mechanics than classical physics and instead represented the conjunction of the two bases as the intersection.
Is a false statement. Voila! John von Neumann and George Birkhoff showed that quantum mechanics necessitates that orthogonal components are simultaneously true and false. Why would two of the worlds most prominent mathematicians believe in such nonsense? von Neumann and Birkhoff really did believe these calculations were correct but it's probably resolvable, there are a whole variety of different ways of answering their argument.
I'll just consider a couple of them that I find convincing. Previously I talked about the contextuality of quantum measurements, not only is one unable to measure both components of spin simultaneously but the spin of a particle does not exist until measured in some interpretations (Copenhagen, Bohmian mechanics, Many Worlds Interpretation). Further more even if they intersect on the Hilbert space, incompatible properties of a quantum system do not need to be combined if one adopts further rules into quantum theory, such as the single family rule (Consistent Histories). Which I've discussed in previous posts.
Although I reject the case made by von Neumann and Birkhoff I don't want to misrepresent quantum logic. What von Neumann and Birkhoff proposed is one argument for one version of quantum logic. Other versions with far more sophisticated arguments exist.
Consider the following 2-Dimensional Hilbert space for particle of half integer spin (all given in units of reduced Planck's constant)
In the Hilbert space the component P is a projection operator and operators orthogonal to each other represent "non community operators" which are incompatible properties of a quantum system.
If P is a projector we can represent its negation as
Now simply, the components P refers to a particle with spin in the z-direction.
Whereas its orthogonal component refers to the same particle with a spin in the z-direction of
Every ray in the Hilbert space represents some value of the spin of the particle which leads to an obvious problem for quantum mechanics. To understand this lets relabel the positive spin in the z-direction with the label P and the negative spin in the x-direction, Q. How do we represent the conjunction of P and Q? In propositional logic the answer is
In propositional logic the conjunction of two contradictories is false, the problem in quantum mechanics is that it's not even false. The statement is undefined because it cannot be represented on a Hilbert space. Von Neumann and Birkhoff began applying different rules to quantum mechanics than classical physics and instead represented the conjunction of the two bases as the intersection.
What is the intersection? Simple, they only intersect at the zero vector. Now we have meaning to this statement and turns out to agree with propositional logic, the statement is false. Whatever basis you choose it is always orthogonal to the zero vector, so it is always false. The same applies to the conjunction of the negative spin in the z-direction with the positive spin in the x-direction.
In all of these rules of quantum mechanics we encounter a complete contradiction.
We can drop the "x-negative spin or x-positive spin" term given that it's always true. But the left hand side of the equation is always false. Which entails that "z-positive spin" is false. We could easily substitute terms to show that
I'll just consider a couple of them that I find convincing. Previously I talked about the contextuality of quantum measurements, not only is one unable to measure both components of spin simultaneously but the spin of a particle does not exist until measured in some interpretations (Copenhagen, Bohmian mechanics, Many Worlds Interpretation). Further more even if they intersect on the Hilbert space, incompatible properties of a quantum system do not need to be combined if one adopts further rules into quantum theory, such as the single family rule (Consistent Histories). Which I've discussed in previous posts.
Although I reject the case made by von Neumann and Birkhoff I don't want to misrepresent quantum logic. What von Neumann and Birkhoff proposed is one argument for one version of quantum logic. Other versions with far more sophisticated arguments exist.

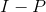






Comments
Post a Comment